앳코더90 - 036 - Max Manhattan Distance（★5）

https://atcoder.jp/contests/typical90/tasks/typical90_aj

036 - Max Manhattan Distance（★5）

 

N개의 x,y로 점의 좌표가 주어지고 Q개의 쿼리가 주어진다. 쿼리에 해당하는 좌표와 가장 맨해튼거리가 먼 점의 거리를 구하라.

 

문제를 읽고 몇 분동안 생각해보다가 내가 아는 알고리즘에서는 풀 수 있는 방법이 없는것 같아 해설을 봤는데, 해설코드로도 이해가 안되서 gpt와 함께 분석까지 했다. 우선 내가 접근한 방식은 무슨 수를 써서도 O(N^2)보다 깎아낼 수 가 없었다. 해설은 다음과 같이 표현한다. 

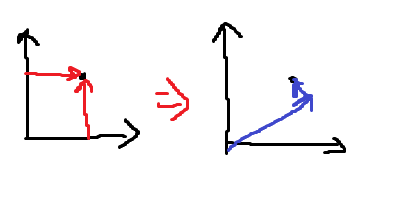
맨해튼 거리 자체를 좌표를 45도 비틀어서 생각하는 것이다. 선형대수학에서 배우는 벡터를 생각해보면 된다. x,y라는 벡터를 x+y, x-y 형태로 만들면 다른 점에서의 벡터가 되고 이를 통해 맨해튼 거리를 N^2으로 계산하지 않아도 된다.

 

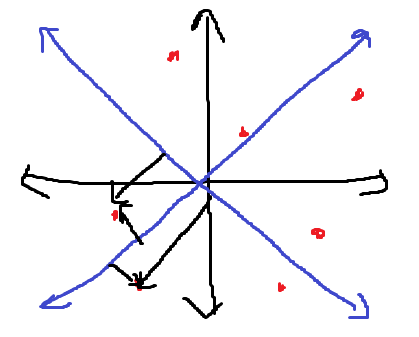
맨해튼 거리를 찾기위해서 |X1-X2| + |Y1-Y2|를 해야되는 것을 X′=X+Y,Y′=Y−X 형태로 간소화한것이다. 변환된 좌표에서의 맨해튼 거리는 기존의 좌표와 당연히 동일하고, 최대 최소값을 구해 O(N)에 각 좌표들 끼리 계산할 수 있다.

 

#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
#include <unordered_set>
#include <numeric>
#include <random>
#include <iostream>
#include <unordered_map>

#define rep(i, n) for (int i = 0; i < (int)(n); ++i)
#define rep1(i, n) for (int i = 1; i <= (int)(n); ++i)
#define range(x) begin(x), end(x)
#define sz(x) (int)(x).size()
#define pb push_back

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<long long, long long> pll;
typedef vector<int> vi;
typedef vector<long long> vll;

const int INF = 2000000000;
const double pi = 3.14159265358979;
const int MOD = 100000;

void yesno(bool a)
{
	if (a)
		cout << "YES\n";
	else
		cout << "NO\n";
}

ll N, Q;
vll x;
vll y;
vll t;
ll minX = LLONG_MAX;
ll minY = LLONG_MAX;
ll maxX = -LLONG_MAX;
ll maxY = -LLONG_MAX;

int main()
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	cin >> N >> Q;

	x.resize(N+1);
	y.resize(N+1);
	t.resize(Q+1);

	rep1(i, N)
	{
		cin >> x[i] >> y[i];
	}
	rep1(i, Q)
	{
		cin >> t[i];
	}

	rep1(i, N)
	{
		ll a = x[i] + y[i];
		ll b = x[i] - y[i];

		x[i] = a;
		y[i] = b;
		minX = min(minX, x[i]);
		maxX = max(maxX, x[i]);
		minY = min(minY, y[i]);
		maxY = max(maxY, y[i]);
	}

	rep1(i, Q)
	{
		ll a = abs(x[t[i]] - minX);
		ll b = abs(x[t[i]] - maxX);
		ll c = abs(y[t[i]] - minY);
		ll d = abs(y[t[i]] - maxY);
		cout << max({ a,b,c,d }) << "\n";
	}
	

	return 0;
}

 

따라서 코드는 위와 같다. 이 개념을 모른다면 절대 풀수없는 문제 같다.